※クリックで全体表示。 |
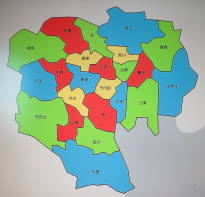
東京23区を4色で塗り分けた図。↓の記事参照 |
|
Copyright(C)長谷川芳典 |

※クリックで全体表示。 |
東京23区を4色で塗り分けた図。↓の記事参照 |
【小さな話題】笑わない数学(1)四色問題(1)中高生の頃に考えたこと 2022年に初回放送され、2023年4月〜6月に再放送された表記の番組についての感想・考察。この番組のシーズン1は、
なお、このことで思ったが、最近のYouTube解説動画はなかなか秀逸で分かりやすい内容になっている。今回の放送は「パンサーの尾形貴弘が難解な数学の世界を大真面目に解説する」というスタイルになっていてそれはそれで良いのだが、「ゆっくり霊夢」と「ゆっくり魔理沙」などがBGMつきの掛け合いで解説をすすめるYouTube動画のほうが分かりやすく、しかもオンデマンドでいつでも見られるという点で長けているようにも思われた。オンライン授業なども、講師がダラダラ喋るよりはゆっくり解説型にしたほうが理解度が高まるかもしれない(←といっても私などには解説動画が作れるほどの才能は無い。) 前置きが長くなったが、上記のような事情で、このWeb日記では#3「四色問題」以降の放送回について感想・考察を述べることにしたい。ちなみに、四色問題(正確には『四色定理』)を解説したYouTube動画としては、 ●【ゆっくり解説】こんなに単純な問題がなぜ100年以上数学者たちを悩ませたのか−四色問題 というのがあった。動画時間は23分46秒となっていて30分番組の『笑わない数学』より短いにもかかわらず、より詳しい情報を提供していた。なお動画に登場しているのは「ゆっくり霊夢」と「ゆっくり魔理沙」ではなく、『ノワール(聞き手)』と『ブラン(解説者)』というキャラになっていた。名前の由来については、フランス語の黒と白、ということ以外にはよく分からない。 さて、四色定理が証明されたのは1975年であり、私が中高生の頃(1965年4月〜1971年3月)はまだ未解決問題であり、私もそれなりにチャレンジしたことがあった。 当時の記憶は曖昧であるが、確か、以下のように考えていたと記憶している。なお、以下、着色する領域は「国」と呼ぶことにする。まず、 ●地図上の任意の国を選ぶ。これをA国とする。A国は通常、複数の国で囲まれている(1つの島全部、あるいは半島の先端にある国などを除く)。A国を囲む国が偶数個であればA国を含み3色で塗り分けが可能であるが、奇数個であれば4色が必要となる。A国を取り囲む国の数はこれで尽くされており、5色が必要になる場合はない。 ということから、 ●地図上のどの国を選んでも、それを取り囲むすべての国を含んだ領域は4色で塗り分けられる。任意の国についてこれが成り立つので、すべての国にあてはまる。よって四色定理は証明された。 と単純に考えた。しかしこれは間違いであることがすぐに分かる。 ここで「証明」されたのは、あくまで、A国とそれを取り囲んだすべての国という範囲に限って4色で塗り分けが可能であるということに過ぎない。 上掲の東京23区の塗り分けを例にすると、千代田区とそれを取り囲む、中央区、台東区、文京区、新宿区、港区までの領域に限定すれば確かに4色の塗り分けは可能であると証明できるが、さらにその外側を囲む、江東区、墨田区、荒川区、北区、豊島区、中野区、渋谷区、品川区の色を塗り分けていく時に、それらが既出の4色の範囲内で確実に塗り分けられるかどうかは何とも言えない。そもそも、上記の千代田区の周りの「国々」が最大3色で塗り分けられる(千代田区を含んで合計4色以内)というのは、中心にあたる千代田区が一色であるからこそ言えるのであって、すでに3色が使われている台東区、文京区、新宿区、港区のさらに外側を囲む「国々」の色を決める際に、隣接する区と同じ色にならないような色が選べるかどうかは全く保証されていないからである。 ということで、さらに考えを発展させて、 ●任意に選んだA国とそれを取り囲んだすべての国という範囲に限っては4色で塗り分けが可能である。これをA国の『A国4色圏』と呼ぶ。次に、またまた任意にB国を選ぶ。B国にも『B国4色圏』が存在する。 と考える。ここで、『A国4色圏』と『B国4色圏』は、
というところまでは考えが進んだのだが、しょせん、天才的数学者たちが100年以上かかっても解けなかった難問を私が解けるわけがない。 次回に続く。 |