※クリックで全体表示。 |
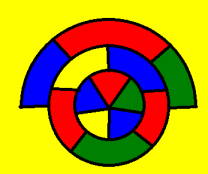
こちらに紹介されていた『ド・ラ・ヴァレ・プーサンの反例』(1896年)。ケンプ鎖の方法で4色に塗り替えることができない最小反例とのことであるが、単に4色に塗り分けるだけであれば画像のように簡単にできる。 プーサンの業績についてはこちらに解説あり。複素解析の方法を使用して素数定理を証明したことなどで知られている。 |
|
Copyright(C)長谷川芳典 |

※クリックで全体表示。 |
こちらに紹介されていた『ド・ラ・ヴァレ・プーサンの反例』(1896年)。ケンプ鎖の方法で4色に塗り替えることができない最小反例とのことであるが、単に4色に塗り分けるだけであれば画像のように簡単にできる。 プーサンの業績についてはこちらに解説あり。複素解析の方法を使用して素数定理を証明したことなどで知られている。 |
【連載】笑わない数学(7)四色問題(7)高齢者でもわかる『最小反例』 昨日の日記で、最小反例の、二辺国、三辺国、四辺国、五辺国について、「もし、○辺国を含む地図で最小反例があったとすれば、どういう矛盾が起きるのかを順に指摘していくというロジックについて述べた。例えば二辺国の場合は以下の通りとなる。
しかし、このロジックは当初、高齢化により頭の回転が鈍くなった私にはよく分からないところがあった。すなわち、 ●5色を使わないと塗り分けられない地図があったと仮定しているので、この地図のどこかには依然として5色が必要は領域が残っているはずだ。なのにどうしてその領域には言及せず、二辺国だけに目を向けているのか? という疑問である。ネットで検索してみたが、この疑問について解説しているサイトは見つからなかった。数学がよく分かっている人たちにとってはあまりにも当たり前であり、そもそも疑問自体が生まれないということかもしれない。 その後、私自身もある日とつぜん「あっ、そういうことだったのか!」と、最小反例のロジックに気づくことができた。そこで、以下に、「高齢者でもわかる『最小反例』」というタイトルで、その内容を記すことにしたい。なお「高齢者でもわかる」というのは単に「高齢者の私でもわかる」という意味であり、「中学生にもわかる」としても趣旨は変わらない。「サルでもわかる」でもよいのだが、さすがにサルでは分からないと思う。 まず、この背理法の仮定は、 ●5色なければ塗り分けられない(平面)地図が存在する と仮定することにある。しかし、国の数が全部で3つとか4つとかの地図は必ず4色で塗り分けられる。なので、上記の仮定は、 【仮定1】nカ国の地図の中には4色では絶対に塗り分けられない地図が存在する という仮定に置き換えることができる。このnの最小値が存在すれば最小反例になり、またnが存在しなければ仮定は間違っていたことになる。ちなみにこの【仮定1】は、次の【仮定2】と両立しなければならない。 【仮定2】n-1カ国の地図は必ず4色で塗り分けられる なぜならば、もしn-1カ国でも絶対に5色が必要という地図があったとすると、nが最小値であるという仮定に反するからである。 以上をふまえたうえで、二辺国、三辺国、四辺国、五辺国の順に検討していくことになる。ここでなぜ六辺国以上は検討しなくても良いのかと言えば、六辺国以上が含まれている地図であっても、オイラーの多面体定理によりそのどこかには五辺国以下の国が少なくとも1つ含まれているからである。例えば蜂の巣のようにすべての国が六角形の形で隣接している地図はすべてが六辺国であるように思われるがこれは無限に広がっている場合の話。その世界の果てにある国は三辺国または四辺国になっていることが分かる。 なお、放送では、あらゆる地図を二辺国、三辺国、四辺国、五辺国という4つの箱に分類していたが、中には二辺国と三辺国の両方を含む地図もあるのでこれは正確ではない。正しくは、
さて上掲の二辺国の場合の検討であるが、もう一度、そのプロセスを再掲すると以下のようになる。
同じ方法は三辺国でも使える。なぜなら、例えば、A、B、Cという3国に囲まれたD国を消滅させたあとで復活させた場合、D国は周りを3色で囲まれていることから4色目で塗れば塗り分けが完成できるからである。 いっぽう四辺国となるとそうはいかない。そこで登場するのが『ケンプ鎖』ということになる。 次回に続く。 |