※クリックで全体表示。
|
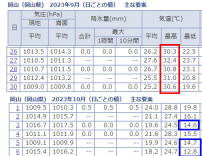
今年の9月は月末まで厳しい残暑が続いていたが、10月に入って一転して秋らしい気候になった。画像は岡山市の9月終わりと10月初めの気温を比較したもので、9月終わりの5日間は連日最高気温が30℃以上の真夏日になっているのに対して10月以降は一度も30℃には達せず、また最低気温が15℃を下回る涼しさとなった。 これに合わせて私も、室内ではランニングシャツのみから長袖ポロシャツに、また短パンを長ズボンに切り替えた。 |
|
Copyright(C)長谷川芳典 |
※クリックで全体表示。

|
今年の9月は月末まで厳しい残暑が続いていたが、10月に入って一転して秋らしい気候になった。画像は岡山市の9月終わりと10月初めの気温を比較したもので、9月終わりの5日間は連日最高気温が30℃以上の真夏日になっているのに対して10月以降は一度も30℃には達せず、また最低気温が15℃を下回る涼しさとなった。 これに合わせて私も、室内ではランニングシャツのみから長袖ポロシャツに、また短パンを長ズボンに切り替えた。 |
【連載】笑わない数学(2)虚数(18)虚数以外の新しい数(9)数とは何か(3)関係概念としての順序、数としての順序 昨日の続き。今回で最終回。 昨日の日記の終わりのところで、Bingに「グラフは数ですか?」という質問をさせていただいたところ「「グラフ理論」における「グラフ」は、関係性を表現するための抽象的な概念であり、数学的な「数」ではありません. 」という回答をいただいた。このことでふと思ったが、順序尺度などで扱われる「順序」はどこまで数と言えるのだろうか? ネットでざっと検索したところ、ウィキペディアには『順序集合』という項目があり、さらに『順序体』とか『順序群』という概念も研究されていることが分かった。なかなか奥が深い。なお、数と数でないものを区別するには、そもそも「元とは何か?」という定義まで立ち返ってみる必要がありそうだが、これはもはや私自身の理解力では歯が立たないように思われた。 それはそれとして、上掲の「グラフは関係概念であるので数ではない」というのが正しいとすると、順序も関係概念なので数とは言えないということになりはしないか?という気がしてきた。但し、ここでいう「関係概念」というのは数学ではなく、行動分析学で扱われる『関係反応』に由来するものである【こちらの文献参照】。大ざっぱに言えば、関係概念というのは、 ●それ自体の特徴としては定まらないもの。他と比較して初めて決まるもの。 というような意味である。 例えば陸上の走り幅跳びで、ある選手が9メートルという大記録を出したとする。飛び終えた時点でその記録は世界記録となるが、その選手が金メダルをとれるかどうかはまだ分からない。あとから跳んだ選手が9メートル1センチ、さらにまた別の選手が9メートル2センチという記録を出したとすると、9メートルを跳んだ最初の選手は銅メダルで3位という順位になる。このように、絶対記録自体はそのモノやコトに固有の性質として測定できるが、順位というのはすべての選手が競技を終えた時点にならないと確定できない。他の選手との比較が必須であるという点で順位は『関係概念』であると考えることができる。 また、リンゴがランダムにいくつか入った籠が10籠あったとする。そのうちの1つに7個が入っていた場合、「7」という個数は絶対的であって他の籠があってもなくても変わることはない。しかしリンゴがたくさん入っている順番に籠を並べた場合、いま述べた7個入りの籠が何番目に多いのかということは、他の籠の個数をすべて調べてみないと確定できない。この場合もやはり、「何番目に多いか」という順位は関係概念になる。 もっとも、見方を変えれば、リンゴの個数自体も関係概念と言えないわけではない。例えば「お皿に3個のリンゴがある」と言う時、1個1個のリンゴの化学的な成分をどんなに調べても「3個」という特徴は出てこない。「3個」というのは、お皿の上にある個々のリンゴの関係性に基づく概念ということになるだろう。 もとの数学の話題に戻るが、数学で扱われる順序というのは、すでに順位が割り振られたあとの「数」の構造であるかもしれない。それに対して走り幅跳びの記録やリンゴの個数の順位というのはその前段階の「順位づけをする方法」を述べたものであった。なので、順位付け自体が相対的なものであっても、そこから抽象化された順位そのものの構造や特徴は別物であるかもしれない。 ここからは余談であるが、心理統計学の授業ではしばしば「順位は順序尺度なので平均できない」と言われることについて、私の考えを述べることにしたい。 「順位は平均しても意味がない」というのは、例えば国際大会に何度も出場している選手と、地方大会しか出ていない選手の「平均順位」を比較するような場合に該当する。地方大会しか出ていない選手のほうが平均順位が少なかった(上位であった)としても、その選手のほうが強いとは言い切れない。このこともあって、ゴルフやテニスなどのプロの選手を比較する時には平均順位ではなく獲得賞金ランキングに言及されることが多い。 では、常に同じメンバーが参加している個人競技の中での平均順位はどうか。この場合、大ざっぱに言って、平均順位の少ない(上位であった)選手のほうが実力があるという推定はできるように思われる。但し、順位を平均するということは、「2回の競技で1位と3位になった」ことと「2回とも2位になった」ことは同程度の実力があるという仮定を認めることになる。もしその仮定に異論がある場合は、重み付けをした上での平均をとる必要がある【←例えば1位は1点、2位は5点、3位は20点というように重み付けした上で平均点が少ないものを上位とする】。 このほか、11時開店の人気ラーメン屋さんの入口に並ぶ時、10時50分に到着した時に行列の何番目になるのかというような順位は平均することに意味がある。なぜなら行列が何番目かということは、10時50分前に来た人が何人いたのかという人数と同じ意味になるからである。なので、何回も並んだときの順番からその平均値や分散を計算すれば、店内の座席数との関係から、開店時にすぐに着席できる確率を推定することができる。 ということで本題から大幅に逸れてしまったが、元の話題の「順位は数か?」に関して言えば、そう言って間違いないようには思う。但し、統計学で、4つの尺度水準の性質に、 名義尺度 ⊃ 順序尺度 ⊃ 間隔尺度 ⊃ 比率尺度 という関係があるとされているのはあくまで、「高い水準はより低い水準の性質を含む形になっている。また高い水準でのデータを低い水準に変換して扱うことができる。」というようなデータ処理上の適用基準のようなものであって、数学で言う「数」は必ずしも、 質的分類(頻度など) ⊃ 順序 ⊃ 間隔 ⊃ 比率 という包含関係にはなっておらず、複素数を導入した時点で「大きさの比較」を犠牲にしたと言ってよいのではないかと思われる。 |