※クリックで全体表示。 |
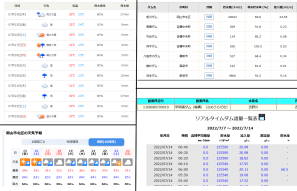
7月9日の日記で「本当の梅雨明けはいつ?」という話題を取り上げたが、その後も「戻り梅雨」模様の天気が続き、この先7月22日頃まではスッキリしない天気が続くものと予想されている。 このおかげで、岡山県・旭川ダムの貯水率は69.6%まで上昇、また四国の早明浦ダムの貯水率も60.5%まで戻った。 今後心配されるのは梅雨末期の豪雨。7月14日は特に警戒が必要とされている。 |
|
Copyright(C)長谷川芳典 |

※クリックで全体表示。 |
7月9日の日記で「本当の梅雨明けはいつ?」という話題を取り上げたが、その後も「戻り梅雨」模様の天気が続き、この先7月22日頃まではスッキリしない天気が続くものと予想されている。 このおかげで、岡山県・旭川ダムの貯水率は69.6%まで上昇、また四国の早明浦ダムの貯水率も60.5%まで戻った。 今後心配されるのは梅雨末期の豪雨。7月14日は特に警戒が必要とされている。 |
【小さな話題】「ランベルトの連分数」と、tan x が有理数になるための必要十分条件 昨日の日記の最後のところで、 と述べた。その後、ネットで検索をしたところ、上記に関連する定理として、 ●有理数である x(x≠0) に対する値 tan x は無理数である という定理(ランベルト,1768, 1770; ルジャンドル, 1794)があることを知った【解説記事はこちら】。 もっとも、上記の定理のtan xのxというのは2パイで一周となるラジアン(弧度法)の表記である。もしそうでなくて、xが360°で一周を表す角度の値(度数法)であるなら、「tan1°は有理数か」という史上最短の入試問題は、ランベルトの定理を使ってあっさりと証明できてしまうのだが、そうはいかない。また、上記の定理はx(ラジアン)が有理数である場合はtan xが必ず無理数になると言っているだけであって、xが無理数の場合にtan xが無理数になるのか有理数になるのかについては何も述べていない。 じっさいのところ、tanを表す直角三角形の直角を挟む辺をaとb、斜辺をcとした時、aとcが挟む角X°が
なお、上記のランベルトの定理の発展として、 ●有理数y に対する値 x = arctany は無理数になる。 も証明されているという。私の理解が正しければ、このことは、もしtan xが有理数であるならば、xは無理数になることを示す。 もっとも、このことで気づいたが、360℃を一周とする角度表示はラジアンで表すと、 x = 2πX°/360 ということになる(小文字xはラジアン、大文字X°は角度)。 要するに、1°から360°までの1°刻みで表す角度というのは、常に無理数πに有理数を掛け合わせたものであり必ず無理数になる。ラジアンで有理数になる角度というのは、例えば「360/π」というように角度自体が無理数となることが分かる。ちなみに「360/π」は「114.591559...」°になるが、これが何か特別な意味(「作図可能」とか)を持つことは考えにくい。なぜなら、もともと「一周=360°」という時の「360」というのは人間が勝手に決めた値であって、別段、一周を100°であるとしても、e°であると決めても本質は変わらないからである。 元の問題に戻るが、元の問題: ●tanX°が有理数となるためのXの条件を述べよ。 を度数法ではなく弧度法に書き換えると、 ●tan x が有理数となるためのxの条件を述べよ。 となる。ここで「ランベルトの定理」(←ランベルトが導き出した定理ではあるが公式にそう呼ばれているのかは分からない)から、 ●xは無理数でなければならない というのが必要条件となるが、これは十分条件ではない。ここまでは隠居人的考察で分かってきたのだが、では、 ●xがどんな無理数であれば、tan x は有理数になるのか? つまり、tan x が有理数になるための必要十分条件は何か?については考え中。 次回に続く。 |