※クリックで全体表示。 |
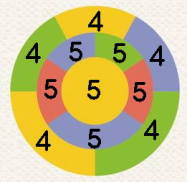
1つの大陸にn個の国があったとする。海に接している国を『海岸国』と呼ぶことにする。図は海岸国がすべて四辺国になる例。↓の記事参照。 |
|
Copyright(C)長谷川芳典 |

※クリックで全体表示。 |
1つの大陸にn個の国があったとする。海に接している国を『海岸国』と呼ぶことにする。図は海岸国がすべて四辺国になる例。↓の記事参照。 |
【連載】笑わない数学(10)四色問題(10)最終回 昨日に続いて、表記の番組の#3『四色問題』の話題。本日で最終回。 まず、昨日の日記で、 これまで論じられてきた地図というのはすべて、何らかの大陸が分割されて構成された地図であった。この場合、大陸が1つであれば、海に接している国は必ずループ状になる。これを仮に『海岸国』と呼ぶことにする。いっぽう、「すべての地図は二辺国、三辺国、四辺国、五辺国のうちのいずれかを含まなければならない」という場合、その二辺国〜五辺国は海岸に接しない内陸国として描かれることが多いように思われる。そもそも、と述べたことについてその後考えてみたが、上掲の図のように、海岸国がすべて四辺国であるような地図はちゃんと存在する。その図の内側にある「5」と書かれたリング状の国々のそれぞれの国境に1つずつ新しい国を挿入すれば海岸国はすべて五辺国となるので、そのような地図が存在することが分かった。但しその場合、新たに挿入された国はすべて四辺国にはなるが。 ここで私が言いたかったことは、 ●すべての国が六辺国であるような地図は存在しない(少なくとも1つの国は、五辺国以下になる)。 という証明だけでは、 ●すべての国が五辺国以上であるような地図が存在する ということは言えないのではないかということであったが、ネットで検索したところこちらのレポートには少なくとも一例、そのような地図があることが描かれていた。ということで私の着眼は徒労に終わった。 ここからは四色定理の一般化についての話題。 放送では全く触れられていなかったが、平面上での四色問題は穴がg個あるドーナツ上の地図の塗り分けに必要な最低限必要な色の数は1890年にヒーウッドによって予想された。ウィキペディアによれば、その式は、 [(7+SQRT(1+48g)/2 ] となっている【[ 」はフロア関数。SQRTは√を表す。参考文献はこちら】。リンゲルとヤングスは1968年にこの予測がg≦1に対して正しいことを証明した。ここでg=0が証明できれば、穴が0個つまり平面上の四色定理の別証明となるのだが、それはうまく行っていないらしい。但し四色定理が証明された現在では、上掲の式はg=0においても成り立つことは言えるのではないかと思われる。 ちなみにg=1の時はドーナツとなるが、この時の式の値は7となる。このほかクラインの壺やメビウスの輪では6となるらしい。 ウィキペディアには、このほかにも「与えられた地図Gに対し、Gを3色で塗り分けできるかどうかを決定せよ」という3彩色問題や、四色問題にかかわるジョークなどが紹介されていた。 四色定理は4年前に又吉直樹のヘウレーカでも取り上げられたことがあった。その際には、4色ボールペンなど直接関係のない話題も取り上げられた。 今後、エレガントな解法で四色定理が再証明されることはありうるとは思う。但しそれはこれまで研究し尽くされてきた領域ではなく、全く別の整数論とか、ポアンカレ予想を証明したペレルマンの手法のような、全く別の視点からの繋がりで証明されることになるだろう。 |